Masina Timpului

 In acest articol voi vorbi despre cum putem construi o masina a timpului care sa produca ceea ce in relativitatea generala se cheama "closed timelike curves", adica traiectorii prin spatiutimp pe care daca le adopti ajungi intr-o continua bucla temporala, calatorind perpetuu catre viitor si totusi ajungand in trecut.

Ideea acestei masini a timpului ii apartine lui Richard Gott, de la Princeton University, care a publicat lucrarea sa in 1991: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.66.1126

Foarte pe scurt, mecanismul este dat de doua corzi cosmice infinite care se deplaseaza una pe langa alta in directii opuse. 

Pentru inceput, este nevoie de doua campuri scalare (scalare in sensul ca nu au o directie in spatiu, ci sunt reprezentate de numere in fiecare loc din spatiu). Un exemplu de camp scalar in realitate este campul Higgs, a carei excitatie este bosonul Higgs. Astfel de campuri scalare sunt ingredientele necesare pentru a avea o coarda cosmica (este nevoie de doua pentru a face aceasta bucla temporala).

Asadar, avem cele doua campuri scalare pentru care avem functia energiei lor potentiale exprimate ca functia energiei lor potentiale data de magnitudinea combinatiei celor doua intr-un singur camp:

Aceasta magnitudine este:

Ceea ce inseamna ca va avea aceeasi valoare daca rotim acest profil in planul Phi1, Phi2 (Phi este litera din alfabetul grecesc care seamana cu "zero").

Profilul densitatii de energie a acestui camp este dat de urmatorul grafic (energia potentiala este pe axul vertical, densitatea de energie este pe axul orizontal):

Si chiar astfel arata campul Higgs, care este un camp care chiar exista in realitate - energia sa potentiala este mai mare la valoarea zero a campului decat la o valoare non-zero. Un astfel de profil poarta numele de "Mexican Hat" sau "Sombrero":

Din cauza ca vidul este dat de orice doua valori care se afla pe cercul definit de valoarea cea mai de jos de pe palaria mexicana, asta inseamna ca nu avem un singur vid - vidul poate fi dat de orice combinatie de Phi1 si Phi2 care sa dea aceeasi magnitudine (vidul se poate afla pe orice punct din cercul marcat cu rosu in imaginea de mai jos).

Genul acesta de profil da nastere posibilitatii existentei unei corzi cosmice. Coarda cosmica descrisa de ilustratia de mai jos "iese din ecran" si depinde de valorile coordonatelor x si y (dar nu si z, coordonata care "iese din ecran"). O astfel de coarda cosmica este descrisa matematic vectorial si arata astfel:

Coarda cosmica se afla in centru, in acel punct rosu. Cercul definit de acele puncte rosii este practic acelasi cu cel rosu de pe palaria mexicana de mai sus, fiind cercul care defineste vidul, cu densitatea de energie zero la acea distanta fata de centru. Asta inseamna ca toata energia campului se afla in interiorul acestui cerc (evidentiata cu galben):

Acum intrebarea este "ce face un astfel de obiect in spatiutimp, conform relativitatii generale?". Efectul este ca coarda cosmica nu produce niciun fel de perturbatii locale in spatiu (cu exceptia centrului), insa produce un "unghi de deficit", adica circumferinta cercului descris de cercul punctat de mai sus este mai mica de 2*pi*r (diferenta fata de origine). Grafic, arata astfel:

In ilustratia de mai sus, unghiul alfa este unghiul de deficit, iar muchia AB este aceeasi cu muchia AC, in sensul ca daca esti in calatorie catre AC si atingi AC, iesi imediat prin AB. "Felia de pizza" definita de unghiul alfa nu face parte din cerc. Daca inlaturam felia, atunci cercul nostru arata astfel:

Daca unim cele doua muchii pentru a face o figura geometrica intreaga, atunci ajungem sa avem un con:

Pentru ca figura geometrica de mai sus este una continua, nu stim niciodata unde este unghiul de deficit, poate fi oriunde. Cu alte cuvinte, putem "taia" conul oriunde pentru a obtine cercul de mai sus, dar cu felia lipsa in alta parte:

Acum, partea interesanta: cum construim o masina a timpului dintr-o coarda cosmica. 

Sa ne imaginam urmatoarea coarda cosmica si doua puncte sub coarda cosmica, A si B:

Acum sa ne imaginam ca trimitem o raza de lumina din punctul A in punctul B. Evident, o potentiala directie este in linie dreapta, de la A la B. Dar o alta potentiala directie, tot in linie dreapta, este perpendicular pe muchia din stanga a unghiului de deficit alfa. Cum muchia din stanga este identica cu muchia din dreapta, raza de lumina va iesi din muchia din dreapta tot perpendicular, imediat ce va intra prin muchia din stanga, si va ajunge in punctul B, precum in ilustratia de mai jos:

Exista situatii in care traiectoria prin unghiul de deficit este mai scurta decat linia dreapta de la A la B.

Acum sa ne imaginam urmatorul scenariu: o nava spatiala care calatoreste aproape de viteza luminii care ia traiectoria prin unghiul de deficit, nu traiectoria care este o linie dreapta intre A si B. Asta inseamna ca nava respectiva va ajunge din A in B inainte unei raze de lumina emisa in acelasi timp din A catre B.

Sa facem o diagrama spatiotemporala unde pe axa orizontala avem o dimensiune spatiala si pe axa verticala avem dimensiunea temporala. A si B sunt fixe pe dimensiunea orizontala (sunt mereu in acelasi loc din spatiu, pe masura ce timpul trece). Adica in felul urmator:

In pasul urmator, reprezentam grafic raza de lumina, care va calatori pe diagonala, la un unghi de 45 de grade, si va ajunge la destinatie intr-o anumita perioada de timp. Nava spatiala va ajunge putin mai devreme decat raza de lumina. Vom reprezenta deci momentul cand nava spatiala ajunge putin mai devreme decat momentul cand raza de lumina ajunge, adica evenimentul va fi putin mai jos pe axa verticala (reprezentat in ilustratie cu rosu):

In relativitatea restransa, daca doua puncte dintr-o diagrama spatiotemporala sunt "spacelike separated", adica sunt intr-o relatie de asa natura incat ar trebui sa calatoresti mai rapid decat viteza luminii pentru a ajunge din A in B, atunci poti gasi un cadru de referinta din care cele doua evenimente sa fie simultane. Daca ne mutam in cadrul de referinta in care cele doua evenimente sunt simultane, graficul arata astfel:

In acest cadru de referinta, nava spatiala pleaca din A si ajunge in B in acelasi timp. 

Acum sa ne uitam la o diagrama in spatiu, ignorand timpul, din cadrul de referinta in miscare in care cele doua evenimente sunt simultane (nava pleaca si ajunge la destinatie imediat, in timp zero). Insa, datorita faptului ca suntem intr-un cadru de referinta in miscare, coarda cosmica se deplaseaza intr-o directie relativ la noi, in acest caz se deplaseaza spre stanga, lucru notat in ilustratia de mai jos cu mov:

Tot ce am construit pana acum este insa doar jumatate dintr-o masina a timpului. Ajungem din A in B. Insa acum avem nevoie sa ajungem si din B in A, folosind acelasi mecanism. Doar asa putem realiza o bucla temporala. Cum coarda cosmica se deplaseaza spre stanga, daca am vrea sa calatorim din B in A ar trebui sa o prindem din urma, ceea ce este problematic.

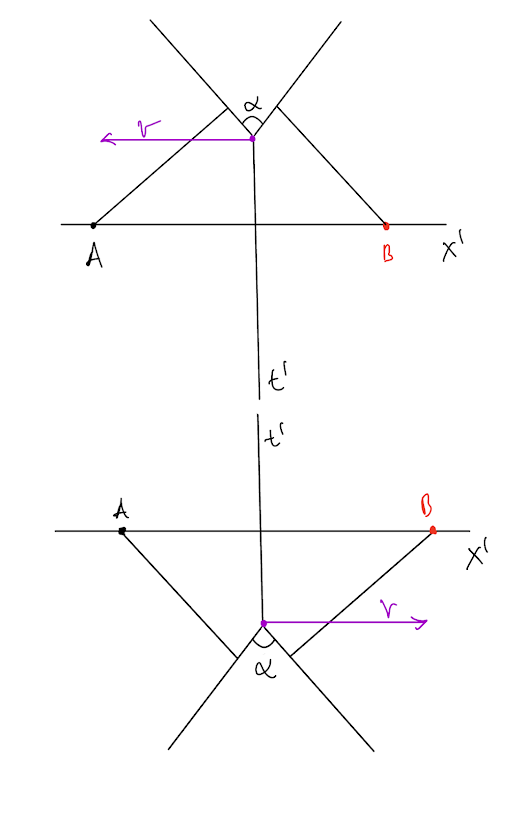
Insa nimic nu ne opreste sa folosim o a doua coarda cosmica ce de data aceasta se deplaseaza in directia opusa pentru a face exact asta:

Intr-o diagrama mai simpla, lucrurile stau astfel:

Alan Guth, Sean Carroll si Ken Olum au descoperit ca intr-un univers deschis, daca iei un sistem de particule care se dezintegreaza radioactiv pentru a face un scenariu similar cu cel de mai sus (pentru ca daca ai doua particule, una in stanga, sa zicem, si alta in dreapta, atunci cand se dezintegreaza emit particule la mare viteza in doua directii opuse, si te poti folosi de acest mecanism pentru a face ceva similar cu scenariul descris de corzile cosmice de mai sus) - nu poti gasi niciun scenariu in care sa poti face o masina a timpului. Motivul este ca intr-un univers deschis, unghiul de deficit maxim este 2*pi si nu ai destula energie pentru a face o masina a timpului. Insa apoi au luat in calcul un alt univers, unul inchis, unde unghiul de deficit este mai mare de 2*pi (intr-un univers inchis sub forma de cub unghiul de deficit este 4*pi). Si au descoperit ca intr-un astfel de univers este posibil sa creezi o pereche Gott de particule care sa produca o masina a timpului si o bucla temporala. Au si adaugat un scurt comentariu lucrarii in care aratau ca intr-un univers deschis este imposibila o astfel de situatie in care au spus ca intr-un univers inchis este posibil.

Insa s-au inselat. Gerard 't Hooft, laureat Nobel, a auzit despre aceasta situatie si a analizat-o mai cu atentie. Ceea ce a descoperit 't Hooft este ca intr-o astfel de situatie, pentru ca universul este unul inchis si poate colapsa, universul respectiv chiar colapseaza inainte ca o masina a timpului sa poata fi construita, in toate situatiile posibile. Cu alte cuvinte, este imposibil sa construiesti o masina a timpului in toate tipurile de universuri.

Natura, deci, pare sa conspire in a interzice construirea oricarei masini a timpului, in a interzice orice situatie posibila care ar duce la o calatorie inapoi in timp. Ceva similar se intampla si in cazul celuilalt mecanism potential care ar putea construi o masina a timpului ce ar permite calatoria in trecut: gaurile de vierme. Se pare ca orice incercare de a folosi o gaura de vierme pentru a calatori in trecut duce la colapsul gaurii de vierme inainte sa apuci sa treci de partea cealalta a sa (de data aceasta pentru ca gaura de vierme necesita o ipotetica materie exotica cu masa negativa, ceea ce nu este compatibil cu trecerea prin ea a unui obiect cu masa pozitiva, asa cum ar fi o fiinta umana).