Cum a salvat mecanica cuantica Universul, partea a IIIa - Atomul lui Schrodinger

Am vazut in prima parte cum aplicarea mecanicii clasice asupra modelului atomic rezulta intr-o catastrofa imediata. Am vazut, apoi, in partea a IIa cum Niels Bohr a cuantizat orbitele electronilor, sau mai bine zis "orbita electronului", asta pentru ca doar atomul de hidrogen cu un singur electron era stabil pentru modelul atomic al lui Bohr.

Ajungem, in sfarsit, pe teritoriul fizicii cuantice. Dar ce inseamna acest lucru? Ce este asa special la scara cea mai mica a naturii? Ce este diferit la scara mica fata de scara intuitiva, fata de scara cosmica?

In fizica, sunt trei tipuri de "scara" la care au loc evenimentele:

1. Scara cuantica: scara la care legile mecanicii cuantice fac legea - scara la care discutam despre particule si interactiunile dintre acestea.
2. Scara clasica: este scara la care obiectele "clasice", cu care suntem obisnuiti in mod intuitiv, interactioneaza: oameni, animale, automobile, bile de biliard si asa mai departe. La aceasta scara, mecanica Newtoniana dicteaza desfasurarea evenimentelor.
3. Scara cosmica: reprezinta nivelul "lucrurilor mari si masive" - stele, planete, galaxii, gauri negre si asa mai departe. Aceasta scara este guvernata de legile Teoriei Generale a Relativitatii, sau, mai bine zis, a poate celei mai mari realizari intelectuale a speciei noastre, prin intermediul lui Albert Einstein.

Din punct de vedere "comportamental", observam o rupere a simetriei naturii in functie de scara la care se desfasoara actiunea: mica, medie sau mare.

O intrebare emerge din acest comportament: este o astfel de diferenta in functie de scara o chestiune naturala, o reprezentare corecta a realitatii?

Din informatiile pe care le-am acumulat pana in prezent, consensul (precar) la nivelul comunitatii stiintifice este acela ca, din moment ce materia este alcatuita din particule, fizica cuantica este de fapt fizica realitatii. Fizica Newtoniana (clasica) ce descrie lumea la scara medie si fizica relativista ce descrie lumea la nivel mare sunt, de fapt, aproximatii ale realitatii, si nu descrieri ad-litteram ale acesteia.

Problema este ca, daca fizica clasica poate fi derivata din mecanica cuantica, ruptura dintre mecanica cuantica si teoria generala a relativitatii este atat de mare incat cele doua nu au putut fi reconciliate pana in prezent. Cu alte cuvinte, cele doua sunt atat de diferite incat nu pot fi unificate matematic. Mai mult, asta previne developarea unei teorii a gravitatiei cuantice - nimeni nu a reusit sa produca o teorie a gravitatiei cuantice (sa descrie cum se comporta gravitatia la cea mai mica scara) inca, desi exista candidati pentru acest lucru (de exemplu, teoria corzilor).

De acum, insa, lucrurile devin foarte, foarte complicate. Si greu de descris. Si greu de disecat pe ce aspecte ar trebui sa ne concentram pentru a face o descriere usor de digerat a mecanicii cuantice. Nu numai ca este contra-intuitiva, asa dupa cum am mentionat de atatea ori de la inceputul acestei serii, dar implicatiile mecanicii cuantice sunt absolut remarcabile, si, ca sa folosim un cliseu, dau valoare expresiei "viata bate filmul". De ce? Pentru ca natura, prin legile mecanicii cuantice, intr-adevar, bate orice fel de film science-fiction ce ar putea fi imaginat folosind doar legile mecanicii clasice.

Daca am fi regizori/scenaristi de filme SF, sau scriitori de romane SF, si ne-am baza imaginatia doar pe fizica clasica, folosindu-ne doar de intuitia umana, am fi foarte, foarte limitati in operele pe care le-am realiza, atunci cand le-am compara cu felul in care realitatea dictata de mecanica cuantica este de fapt.

Ca sa intelegem aceste diferente dintre felul in care materia pare ca se manifesta la nivel clasic si felul in care se manifesta ea de fapt, trebuie sa facem o dihotomie intre comportamentul cuantic si implicatiile comportamentului cuantic.

As dori sa ne concentram asupra comportamentului cuantic in aceasta postare, dupa care sa vedem cum rezolva acest comportament problema atomului Rutherford-Bohr, atom care ori colapsa in 0,02 nanosecunde, ori, in cazul lui Bohr, descria doar atomul de hidrogen.

Newton insusi credea ca lumina este compusa din particule. Mai apoi s-a descoperit ca lumina se comporta, de fapt, ca o unda. La inceputul secolului XX, insa, s-a constatat ca lumina este, de fapt, compusa din fotoni, este cuantizata, si deci este compusa din particule. Despre electron s-a presupus ca este o particula, dar mai apoi s-a descoperit ca are si proprietati de unda! In descrierea unei particule, nu poti spune daca este o unda sau este o particula. Este ambele, si este niciuna dintre ele!

Electronii, de fapt, se comporta ca lumina. La fel si alte particule. Putem spune ca particulele sunt, de fapt, "unde de particula". Ceea ce, evident, la scara clasica, nu are niciun sens. Dar are sens la scara cuantica.

Eroii care au descoperit acest comportament ciudat sunt Erwin Schrodinger, Werner Heisenberg si Max Born.

Erwin Schrodinger

Werner Heisenberg

Max Born

Acesti trei oameni au obtinut descrierea coerenta a comportarii materiei la scara mica, in 1926 si 1927.

Pe scurt, spunem ca la nivel cuantic exista entitati ce sunt intr-o stare de dualitate "unda-particula". Pentru a intelege acest lucru, trebuie sa intelegem celebrul experiment cu doua fante.

Experimentul trebuie descris din 3 puncte de vedere: folosind gloante, folosind unde si folosind electroni.

1) Folosind gloante

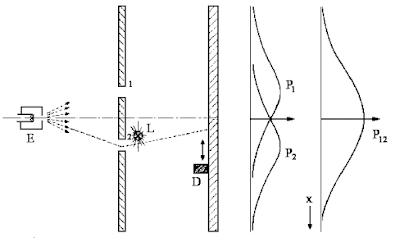
Sa ne imaginam ca avem o mitraliera care trage gloante la intamplare, la diferite unghiuri, catre un perete blindat ce are doua orificii prin care pot trece gloantele. In spatele peretelui blindat avem un alt perete care este lovit de gloante, in cazul in care acestea trec de peretele blindat, prin orificii.

Mitraliera trage gloantele catre perete, la diferite unghiuri,
iar cele care sunt in unghiul ce le permite trecerea printr-unul dintre orificii
vor lovi peretele din spatele peretelui blindat (vor lovi peretele denumit "BACKSTOP").

 In dreapta avem diagramele de probabilitate ca gloantele sa ajunga
in diferite zone ale peretelui din spate: P₁ pentru diagrama de probabilitate
a primului orificiu, si P₂ pentru cea pentru cel de-al doilea orificiu.

Probabilitatea P₁₂ totala, pentru experiment, este suma probabilitatilor, adica
P₁₂ = P₁+P₂

In acest caz, nu putem calcula decat probabilitatea ca un glont sa treaca printr-unul dintre orificii si sa loveasca peretele din spatele peretelui blindat. Astfel, avem o diagrama de probabilitate pentru primul orificiu, P₁, si o diagrama de probabilitate pentru cel de-al doilea orificiu, P₂. Daca acoperim unul dintre orificii, gloantele pot trece doar prin cel ramas neacoperit. Deci, daca acoperim orificiul 2, gloantele trec doar prin orificiul 1 si vom avea doar diagrama de probabilitate P₁. Daca acoperim orificiul 1, gloantele nu pot trece decat prin orificiul 2, si vom avea doar diagrama de probabilitate P₂.

Dupa cum se vede in figura de mai sus, pentru primul orificiu este mai probabil ca gloantele sa nimereasca intr-o mai mare masura pe dreapta ce uneste orificiul 1 si arma, cu oarece sanse din ce in ce mai mici sa nimereasca si "pe undeva in apropierea" acelei zone, fiind deviate de orificiul prin care trec, la diferite unghiuri.

Probabilitatea pentru acest experiment referitoare la gloantele care trec prin cele doua orificii si ajung sa loveasca peretele din spate este pur si simplu suma probabilitatii celor doua orificii, P₁ + P₂. Cea mai mare probabilitate ca gloantele sa nimereasca peretele este in centru, intre orificiile 1 si 2, deoarece atat gloantele care trec prin primul orificiu cat si cele ce trec prin cel de-al doilea vor nimeri in acea zona. Nimic complicat sau greu de inteles. In partea cea mai din dreapta a figurii vedem cum arata grafic aceasta probabilitate.

OK, in experimentul cu gloantele este totul clar si intuitiv. Experimentul cu gloantele arata cum ar trebui sa se comporte un experiment similar cu electroni, daca acestia ar fi particule, "cuante", chestiuni bine determinate, discrete. Trebuie sa reiterez ca nu este nimic "special" la electroni, sau ceva care tine "doar de ei". Putem face acelasi experiment si cu alte particule.

2) Folosind unde pe suprafata apei

Sa presupunem ca facem acelasi experiment folosind de aceasta data unde pe suprafata apei. Avem un generator de unde in apa, undele se propaga catre un perete cu doua fante, iar in spatele acelui perete se afla un alt perete unde putem detecta cu ce intensitate lovesc unele ce trec prin cele doua fante peretele detector, care este "absorbant de unde" (undele nu se reflecta din el).

In acest caz, vedem ca diagrama de probabilitate I₁₂ nu mai este suma
celor doua probabilitati, ci modulul sumei h₁ + h₂ la patrat.

In acest caz, putem avea orice fel de valori pentru intensitatea undei. Unda nu este masurata in "bucati", nu este cuantizata, este un continuu (desigur, facem o aproximatie doar de dragul intelegerii conceptului).

Daca acoperim unul dintre orificii, vom vedea ca obtinem diagramele de la (b), I₁ si I₂, care arata exact ca cele din scenariul cu gloantele. Nu este practic nicio diferenta.

Rezultatul probabilitatii la nivel de experiment, insa, cu ambele fante deschise este cel de la (c), deoarece undele, spre deosebire de gloante, interactioneaza intre ele - sunt in interferenta. In anumite locuri, unde se afla maximele curbei I₁₂, undele sunt in faza, iar maximele lor se aduna dand o amplitudine mai mare si deci o intensitate mai mare. Aceste unde interfera constructiv. Asemenea interferente constructive vor exista oriunde distanta de la detector pana la unul dintre orificii este cu un numar intreg de lungimi de unda mai mare sau mai mica decat distanta de la detector pana la celalalt orificiu.

In locurile in care cele doua unde ajung la o diferenta de faza PI (sunt in opozitie de faza), miscarea ondulatorie rezultanta la detector va fi diferenta celor doua amplitudini. Undele interfera distructiv, si obtinem deci o amplitudine mai mica si o intensitate mai mica a undei. Astfel de valori mici sunt de asteptat oriunde distanta dintre orificiul 1 si detector difera de distanta dintre orificiul 2 si detector cu un numar impar de jumatati de lungimi de unda. Valorile mici pe care le regasim pentru I₁₂ corespund locurilor in care cele doua unde interfera distructiv.

Asadar, diferentele dintre experimentul cu gloante care rezulta in diagrama P₁₂ si cel cu unde pe suprafata apei care rezulta in diagrama I₁₂  sunt evidente, chiar daca rezultatele atunci cand inchidem unul dintre orificii sunt identice - tiparele de interferenta ce exista in cazul undelor dar nu exista in cazul gloantelor fac diferenta, atunci cand ambele orificii sunt deschise.

Sa vedem mai jos cateva exemple de tipare de interferenta:

Intrebarea este - ce se intampla daca facem acelasi experiment cu electroni in loc de gloante?

3) Folosind electroni

Pentru acest experiment construim un "tun electronic" care consta dintr-un filament de tungsten incalzit de un curent electric si inconjurat de o cutie metalica avand un orificiu. Daca filamentul se afla la o tensiune negativa fata de cutie, electronii emisi vor fi accelerati catre pereti si o parte dintre ei vor trece prin orificiu. Toti electronii care ies din tun vor avea aproape aceeasi energie. In fata tunului se afla o placa subtire de metal cu doua orificii, iar dincolo de perete se afla o alta placa servind drept ecran de oprire. In fata acesteia se afla un detector de electroni conectat la un difuzor.

Facand aceasta experienta, primul lucru pe care-l vom constata este acela ca de fiecare data cand un electron loveste detectorul, vom auzi "tic-uri" distincte. Nu exista "jumatati de tic". Tic-urile sosesc, de asemenea, dezordonat: tic-tic... tic... .... tic-tic-tic-tic... tic... .... ........ .... tic.... tic-tic-tic-tic-tic.... si asa mai departe.

Totusi, daca este sa masuram cate tic-uri receptionam pentru o durata relativ lunga de timp (de ordinul minutelor, sa zicem), vom avea cam acelasi numar de tic-uri receptionat pentru acea perioada de timp pentru diferite masuratori (sa zicem ca avem 1000 de tic-uri pentru un experiment de 10 minute facut la ora 10:00 - daca repetam experimentul la ora 13:00, tot pentru 10 minute, in ciuda caracterului aparent aleator al tic-urilor, vom avea o suma foarte similara celor 1000 de tic-uri din primul experiment, sa zicem vom avea 989 de tic-uri sau 1008 tic-uri, dar fara deviatii subtantiale de la norma de "1000" masurata prima data).

Daca deplasam detectorul de-a lungul peretelui de oprire, numarul tic-urilor scade sau creste dar intensitatea fiecarui tic ramane neschimbata. Daca scadem temperatura filamentului din tunul de electroni, ritmul tic-urilor scade, dar fiecare tic continua sa se auda la fel ca si inainte.

De asemenea, daca asezam doi detectori in fata ecranului de oprire, vom auzi un tic intr-unul sau in celalalt detector, dar nu in ambii detectori in acelasi timp (acest lucru va deveni important mai tarziu).

Din toate acestea putem concluziona ca electronii sunt cuantizati, sunt bucati discrete, identice (desigur, stim ca un electron nu este altceva decat o excitatie a campului cuantic de electroni - de aceea fiecare electron are aceleasi proprietati ca orice alt electron de oriunde - este excitatia aceluiasi camp cuantic).

Asadar, se pare ca electronii sunt, intr-adevar, particule, si nu unde. Toate dovezile de pana acum ne duc in aceasta directie.

Daca inchidem una dintre fante si o lasam pe cealalta deschisa, si invers, si masuram probabilitatea distributiei electronilor de la receptor, vom observa aceeasi curba ca si in cazul gloantelor dar ca si in cazul undelor (repet, cu un singur orificiu deschis, nu cu ambele). Putem face presupunerea ca fiecare electron este o particula care trece, atunci cand deschidem ambele orificii, ori prin orificiul 1, ori prin orificiul 2, intocmai gloantelor.

Ce se intampla insa daca masuram curba de probabilitate a electronilor emisi atunci cand ambele orificii sunt deschise? Obtinem curba valabila pentru undele la suprafata apei, si nu pe cea pentru gloante! Avem un tipar de interferenta care este valabil in cazul undelor, nu in cazul particulelor!

Vi se pare o diagrama cunoscuta? Este intocmai diagrama din cazul undelor
la suprafata apei, si anume rezultatul P₁₂ este identic
cu I₁₂ pe care l-am avut in cazul experimentului
cu undele la suprafata apei!

Cum poate fi asa ceva posibil? Cum pot electronii sa se prezinte avand caracter de particule, de "cuante", de "bucati discrete", si totusi sa afiseze un tipar de interferenta care este caracteristic undelor?! Este intocmai aceasta dualitate unda-particula acel lucru care da caracterul misterios al fizicii cuantice. Dar este oare asa?

Considerand tiparul de interferenta, se pare ca electronii sunt, de fapt, unde. Ce se intampla insa daca incercam sa urmarim electronii?

4) Folosind electroni insa urmarindu-i

Daca incercam insa sa trisam? Daca incercam sa "vedem" unde este electronul? Punem o sursa de lumina de mare intensitate (multi fotoni) in spatele peretelui cu cele doua orificii, in centru. Atunci cand electronul trece printr-unul dintre orificii, el va lovi in drumul sau un foton, iar noi vom putea vedea din ce directie vine acel foton si deci vom putea determina prin care dintre orificii a ales electronul sa treaca. Suna bine.

Am pus o sursa de lumina "L" in spatele peretelui cu cele doua orificii.
Sarcinile electrice imprastie lumina. Atunci cand electronul trece printr-unul dintre
orificii, el va face o "scanteie" si vom putea identifica prin care dintre orificii a trecut.

Ce vom observa daca facem acest experiment? Vom vedea "unda de electroni"? Vom vedea ca electronul se imparte in doua si trece prin ambele orificii?

De fiecare data cand auzim un "tic" in detectorul nostru, vedem si o scanteie care provine ori din vecinatatea orificiului 1, ori din vecinatatea orificiului 2, dar niciodata din ambele in acelasi timp. Acest lucru este consistent, oriunde asezam detectorul vom obtine acelasi rezultat. Putem deci concluziona ca electronul trece printr-un singur orificiu, si se comporta ca o particula.

Daca ne notam prin ce orificiu a trecut electronul si unde l-am receptionat in detector, obtinem din nou curbele P₁ si P₂. Aceleasi curbe pe care le-am obtinut si in experimentul cu gloantele, atunci cand am inchis orificiul 1 si orificiul 2, lasandu-l pe celalalt deschis, dar si in cazul undelor prin apa, la fel, cand am avut doar un singur orificiu deschis. Nimic suprinzator.

Ce se intampla insa cu probabilitatea totala a locului unde ajung electronii? Pai ce sa se intample? Probabilitatea totala devine suma probabilitatilor P₁ si P₂, asadar P₁₂ = P₁+P₂, intocmai ca in cazul experimentului cu gloantele! Unde este curba de probabilitate ce prezenta interferenta, ca in experimentul cu numarul 3, atunci cand nu aveam sursa de lumina? Nu mai este. Acum electronul se comporta ca o particula, ca un glont.

Ce se intampla daca "stingem lumina", daca oprim sursa de lumina? Obtinem din nou, atunci cand masuram curba totala, aceeasi interferenta pe care o obtineam la experimentul cu numarul 3. Cu alte cuvinte, atunci cand electronul este "urmarit", el nu se mai comporta ca o unda ci devine o particula!

Dar daca scadem intensitatea luminii? Poate ca lumina interactioneaza cu electronul si-l perturba din directia sa, in vreun fel. Daca scadem intensitatea luminii, primul lucru pe care-l observam este acela ca scanteile nu devin mai slabe - ele sunt la fel de intense. In schimb, cateodata auzim un "tic" in detector insa nu vedem nicio scanteie - electronul a reusit sa treaca fara sa fi fost "vazut". Ce inseamna acest lucru? Inseamna ca si lumina este corpusculara, cuantizata - motivul pentru care electronul a trecut nevazut este acela ca nu s-a ciocnit de un foton, in drumul sau catre detector.

De fapt, scazand intensitatea luminii, asa dupa cum am vazut in partea a IIa a acestei serii, nu am facut altceva decat sa scadem numarul de fotoni ce pot interactiona cu electronul - tineti minte, energia unui foton este produsul dintre constanta lui Planck si frecventa acestuia. Cu alte cuvinte, energia fotonilor emisi este aceeasi, dar numarul lor este mai mic, atunci cand scadem intensitatea luminii (aduceti-va aminte de efectul fotoelectric descris de Einstein).

Haideti sa scadem intensitatea luminii foarte mult -  sa se intample foarte rar ca un electron sa interactioneze cu un foton si sa-l "vedem". Ce obtinem?

In cazul electronilor care au "scanteiat" din directia orificiului 1, obtinem o curba probabilistica P₁. In cazul electronilor care au scanteiat dinspre orificiul 2, obtinem curba P₂. Aceleasi curbe cunoscute, clare, care dau comportamentul electronilor de particula, acelasi cu cel din experimentul cu gloantele.

Ce fac electronii care nu au "scanteiat"? Ei vor da acelasi tipar de interferenta ca in cazul experimentului cu undele la suprafata apei. Electronii care nu au interactionat cu vreun foton, care nu au "fost vazuti", isi vor pastra proprietatile de unda.

Asadar, cand electronii sunt perturbati de catre fotoni, acestia au comportament de particule. Am putea, totusi, sa incercam sa nu-i perturbam, sa nu le distrugem starea de unda? Putem facem cumva sa-i vedem fara a-i perturba?

Impulsul unui foton este dat de formula p=h/f, unde p este impulsul, h este constanta lui Planck iar f este frecventa. La fel de bine putem spune ca E=hf. Fotonul, cu energia sa, loveste practic electronul si-l deviaza de la traiectoria sa. Ca sa scadem lovitura pe care electronul o primeste, va trebui nu sa scadem intensitatea luminii (numarul de fotoni), ci sa scadem frecventa luminii (care va duce la scaderea energiei pe care fotonul o are, si deci la scaderea loviturii primite de catre electron atunci cand electronul si fotonul se ciocnesc).

Astfel, poate ca vom reusi sa nu mai interferam cu electronul atat de mult incat sa-i schimbam traiectoria. Putem, deci, sa folosim lumina infrarosie, sau unde radio, in loc de lumina vizuala. Lumina infrarosie sau undele radio au o lungime de unda mai mare, adica o frecventa mai mica, si cum energia unui foton este produsul dintre constanta lui Plack si frecventa, vom obtine fotoni de energie mai mica.

Folosim lumina cu lungime de unda din ce in ce mai mare, in speranta ca vom perturba electronul din ce in ce mai putin. La inceput nu este nicio diferenta fata de experimentul cand foloseam lumina vizibila. Continuand cu lungimi de unda din ce in ce mai mari, vom ajunge la momentul in care lungimea de unda este mai mare decat distanta dintre cele doua orificii. In acel moment, tot ce putem vedea este o scanteie difuza, o scanteie pentru care nu putem determina daca provine dinspre orificiul cu numarul 1 sau orificiul cu numarul 2!

Fiindca lumina este o unda, nu stim pozitia exacta a fotonului de-a lungul undei.
De aceea, cu cat lungimea de unda este mai mare, cu atat mai incerta este pozitia
fotonului. Daca scadem lungimea de unda marind frecventa, stim mai precis unde se afla fotonul,
dar acesta are energie prea mare si perturba electronul cu care se ciocneste, prabusindu-i functia de unda.

Ce este interesant si, poate, sadic, pentru aceste experiment, este faptul ca lungimea de unda de la care energia fotonului ce interactioneaza cu electronul este indeajuns de mica pentru a nu-l mai perturba (pentru a nu-l mai determina sa se comporte ca o particula, pierzandu-si caracterul de unda) este mai mare decat distanta dintre cele doua orificii, facand astfel imposibila determinarea locatiei evenimentului ciocnirii dintre electron si foton (nu mai putem spune prin care dintre cele 2 orificii a trecut electronul).

Rezulta deci ca este imposibil sa potrivim lumina astfel incat sa stim prin ce loc a trecut electronul fara sa-i perturbam impulsul, si invers. Nu putem stii ambele variabile deodata! Nu putem stii locatia unui electron SI impusul acestuia; putem stii cu precizie doar unul dintre ele. Atunci cand avem o valoare precisa pentru pozitia acestuia, avem o valoare imprecisa pentru impuls. Atunci cand stim impulsul, nu putem determina pozitia.

Acest lucru a fost propus, ca principiu general, de catre Werner Heisenberg, si a fost denumit "principiul de incertitudine". Este imposibil de imaginat un aparat care determina prin ce orificiu trece electronul si care in acelasi timp nu perturba electronul atat de mult incat sa-i distruga figura de interferenta.

Cred ca nu mai este necesar sa spun ca acest fapt este o chestiune remarcabila. Foarte multi oameni de stiinta s-au luptat sa invinga principiul de incertitudine al lui Heisenberg (inclusiv Heisenberg insusi), insa nu a fost posibil. Se pare ca principiul de incertitudine este o realitate, nu are niciun fel de "chichita ascunsa" sau "tric".

De fapt, Albert Einstein insusi avea o mare problema cu maniera in care mecanica cuantica, prin intermediul principiului de incertitudine, se manifesta, spunand celebrul citat:

"Dumnezeu nu da cu zarul" - Albert Einstein

 Interesant este ca unii teologi (rau intentionati) s-au referit la acest citat (si alte citate asemanatoare) pentru a spune ca Einstein era un om religios, sau ca acesta credea in existenta unei divinitati. Aici, Einstein se refera in mod metaforic la natura. Am putea "traduce" acest citat ca "Natura nu poate avea o caracteristica probabilistica" - asa dupa cum putem constata acum, stiind despre principiul incertitudinii.

Niels Bohr i-a dat un raspuns lui Einstein:

"Einstein, nu-i spune tu lui Dumnezeu ce sa faca!" - Niels Bohr

Traducere: "Realitatea este asa cum este, chit ca-ti convine tie sau nu".

Sa revenim la modelul atomic. Am vazut ca modelul atomic al lui Rutherford colapsa dupa 0,02 nanosecunde. Am vazut apoi ca Niels Bohr a cuantizat orbitele electronilor pentru atomul de hidrogen, nepermitand electronului sa aiba o orbita mai scazuta decat cea mai joasa orbita, si deci nepermitandu-i sa colapseze in protonul incarcat pozitiv.

Dar aceste modele atomice nu sunt corecte. Trebuie sa existe o explicatie clara prin care sa intelegem de ce atomii inca exista.

Era evident faptul ca Niels Bohr avea dreptate presupunand ca momentul cinetic este cuantificat pentru electron. Louis Broglie a propus ideea ca electronul, sau chiar toate particulele, au proprietati de unda, ca si fotonul. Poate ca particulele sunt cuantizate similar cu modul in care undele sonore de lunga durata dintr-un flaut vibreaza numai la anumite frecvente speciale.

Va amintiti de interferentele distructive si interferentele constructive din cazul experimentului cu unde pe suprafata apei? Exista unde similare si la suprafata Soarelui, determinate de undele sonore din gazul/plasma fierbinte. Daca o asemenea unda se propaga peste tot in jurul Soarelui, se va anula pe sine printr-o interferenta distructiva, daca nu efectueaza exact un numar intreg de oscilatii in timp ce inconjoara Soarele, pastrandu-si sincronizarea. Rezulta deci ca, la fel ca un flaut, Soarele oscileaza la anumite frecvente speciale.

Apropos, acelasi lucru se intampla si in cazul anvelopelor automobilelor la viteze mari, undele sonore rezultate care circula in jurul camerei in rezonanta ducand la distrugerea pneului.

Broglie a sugerat acelasi lucru pentru atomul de hidrogen, in 1924, si a obtinut exact aceleasi frecvente si energii pe care le-a prezis modelul lui Bohr.

Bun, pana la urma, care este explicatia existentei atomilor, asa cum ii cunoastem? Este o explicatie foarte simpla, acum ca stim toate aceste lucruri, si are legatura, asa dupa cum sunt sigur ca ati ghicit, cu principiul de incertitudine:

Daca electronii s-ar gasi in nucleu, atunci le-am cunoaste pozitia foarte precis. In acest caz, principiul de incertitudine cere ca ei sa aiba un impuls foarte mare si incert, ceea ce inseamna, mai exact, o energie cinetica foarte mare. Energia cinetica ar deveni atat de mare, incat acestia s-ar zmulge din atractia nucleului. Asa ca, pana la urma, electronii fac un compromis in aceasta relatie de incertitudine - nu colapseaza in nucleu, ci se mentin pe orbite superioare (astfel incat sa nu violeze partea pozitiei din principiul de incertitudine), iar in acelasi timp oscileaza cu o anumita cantitate de miscare minima (astfel incat sa nu violeze partea impulsului din principiul de incertitudine).

Acest lucru, dincolo de implicatiile faptului ca ne permite sa existam (permite existenta materiei in Univers), mai are o implicatie interesanta - stim ca temperatura unui obiect reprezinta agitatia termica a acelui obiect - cat de mult se "agita" atomii acelui obiect. Dar sa presupunem ca racim un quartz la temperatura de 0 grade Kelvin (zero absolut). Am putea deduce ca pozitia particulelor din acest quartz este clara - ele sunt stationare, tocmai de aceea are temperatura de 0 grade Kelvin - nu exista agitatie termica in acest obiect. Dar in acest caz am cunoaste pozitia particulelor cu precizie (din moment ce acestea au zero energie cinetica si practic nu se misca) - problema este ca am viola principiul de incertitudine, stiind cu precizie pozitia particulelor, si stiind in acelasi timp ca au energie cinetica zero, si deci nu se misca (au impuls cunoscut). Am cunoaste, deci, si pozitia, si impulsul particulelor din acest obiect. Din acest motiv, atomii acestui quartz racit la 0 absolut trebuie sa se miste - daca stim pozitia lor, ei nu pot face altceva decat sa vibreze, pentru a nu viola principiul de incertitudine!

Tin minte ca acum multi, multi ani in urma (probabil ~15), am fost in vizita cu familia la un prieten de familie, cu studii in fizica, un om foarte inteligent. Si tin minte ca am ajuns sa discutam despre cateva chestii legate de fizica. Un singur lucru mi-a ramas in minte (aveam in jur de 20 de ani) - si anume ca "la inceput a fost vibratia".

Si din acel punct m-am tot gandit la ce a vrut sa zica prin asta. Pentru ca suna foarte "ezoteric" - dar iata ca principiul de incertitudine lamureste lucrurile - avand pozitia clara a unui obiect, acesta este imposibil sa nu vibreze.

Ba mai mult, o alta implicatie a principiului de incertitudine (si a altor principii din mecanica cuantica) duce la existenta constantei cosmologice, sau a dark energy (energia intunecata) - a energiei vidului. Vidul (spatiul gol, complet golit de particule/energie) are o energie - aceasta este energia care duce la expansiunea actuala a Universului. Cum insa acesta este un cu totul alt subiect, pentru un probabil post viitor, nu voi intra in amanunte (pot spune doar ca energia vidului este data de contributia particulelor virtuale care exista la scara Planck, atat temporala cat si spatiala (atat in timp cat si in dimensiune - mai exact, 5.39 * 10^-44 secunde si 1.61 * 10^-35 metri). Cu alte cuvinte, daca aplicam principiile mecanicii cuantice asupra spatiului gol, obtinem ca spatiul gol are energie, energie care duce la expansiunea spatiului.

Acest lucru are, la randul sau, alte implicatii, daca e sa tinem cont de faptul ca scena in care existam, spatiu-timpul, este o geometrie cu 4 dimensiuni, denumita spatiu Minkowski. Intr-un fel, putem zice ca spatiul unui observator poate fi timpul altui observator, in spatiul Minkowski, lucru care a fost inspirational pentru Albert Einstein in developarea Teoriei Speciale a Relativitatii (astfel, spatiu si timpul erau relative la observator, spatiul si timpul erau personale, si nu absolute). Daca este sa aplicam principiile cuantice asupra spatiului Minkowski, oare ce vom descoperi? :)

Nota: Hermann Minkowski a fost profesorul lui Einstein, unul dintre putinii oameni cu adevarat respectati de catre acesta.

Am putea continua la nesfarsit cu implicatiile mecanicii cuantice (de exemplu, implicatiile Universurilor paralele ale lui Hugh Everett, derivate din natura probabilistica a particulelor cu efecte macroscopice), dar este indeajuns ce am discutat in acest post, si-asa destul de lung.

Cert este ca un alt post, in care sa discutam care sunt implicatiile comportamentului cuantic ar putea fi interesant. Poate unul, de ce nu, referitor la Universuri paralele sau, mai corect spus, la Multivers.

Apropos de Multivers - acesta este, de obicei, un lucru relativ usor de inteles. Insa maniera in care majoritatea oamenilor au in gand un multivers (ca fiind doar o colectie de "mai multe Universuri") este cu mult limitata fata de actualul potential real al posibilitatilor "nivelurilor" de Multivers. Dar despre toate acestea, intr-o postare viitoare.

In final, as dori sa mai adaug ca descoperirile si formularile matematice ale lui Born, Heisenberg si Schrodinger, referitoare la mecanica cuantica moderna, nu numai ca au rezolvat problema atomilor ce colapsau, dar au explicat si spectrele atomilor mai complicati si diferitele numere care descriau proprietatile reactiilor chimice. Efectele fizicii cuantice in viata de zi cu zi?

• laserul
• tranzistorul
• circuitul integrat
• computerele
• telefoanele mobile
• teoria cuantica a campurilor

Asadar, acelasi lucru care ne scotea din sarite initial, cand incercam sa gasim pozitia si impusul electronilor din experimentele despre care am discutat, care parea ca ne saboteaza de fiecare data, s-a dovedit a fi chiar faptul existentei atomilor, si deci, a existentei noastre - principiul de incertitudine al lui Heisenberg.

Iar daca prima parte a acestei serii s-a numit "Atomul lui Rutherford" iar cea de-a doua "Atomul lui Bohr", putem numi varianta corecta a modelului atomic "Atomul lui Schrodinger", si arata cam asa:

"Electronii" sunt distribuiti in "norul electronic", adica zona de degradee incetosata. O diferenta mare intre acest model si modelul lui Bohr sau cel al lui Rutherford, nu credeti?