Cum a salvat mecanica cuantica Universul, partea a IIa - Atomul lui Bohr

Asa dupa cum am vazut in prima parte a acestei serii, atomul lui Rutherford, dedus prin intermediul fizicii clasice (fizicii Newtoniene, intuitive), rezulta intr-o mare catastrofa pentru Univers - orice astfel de atom ipotetic, supus legilor fizicii clasice si nu legilor mecanicii cuantice colapseaza in doar 0,02 nanosecunde.

Adevarul este ca in prima parte nici macar nu am discutat despre "fizica cuantica". Asta dintr-o sumedenie de motive - de la complexitatea subiectului la necesitatea intelegerii diferentelor dintre cele doua "fizici" si implicatiile acestora.

Ca sa intelegem modelul atomic al lui Bohr, care vine ca o completare peste modelul atomic al lui Rutherford, trebuie sa intelegem, din nou, mai multe lucruri/concepte/realitati, care, insumate, l-au condus pe Niels Bohr catre crearea acestui model atomic.

Max Planck, parintele fizicii cuantice

In anul 1900, fizicianul german Max Planck a dat, practic, nastere mecanicii cuantice. Mai intai insa, trebuie sa intelegem ce inseamna termenul "cuantic" la modul pragmatic. Il tot folosim strict ca si un termen care exprima o denumire, insa nu il folosim in adevaratul sens al cuvantului. De fapt, este o notiune simplu de inteles:

Sa ne gandim putin la matematica - contine o serie de multimi de numere: naturale, intregi, reale, complexe, irationale si asa mai departe. Unele numere pot avea zecimale, unele numere pot avea o "infinitate" de zecimale.

Teoretic vorbind, putem "folosi", matematic, un numar cu extrem de multe zecimale, ceva de genul: 0,4252852528345789457834583475834728957258169565964623352543583457894578345834728957258695659646237127152526599996956956596462369565964623834535789457834587289572581695657834583472 - intelegeti ideea.

Problema este (si este bine ca exista aceasta problema) - un astfel de numar nu prea are sens in lumea reala. In lumea reala trebuie sa avem cantitati fizice "bine definite". Diferenta dintre un continuu si niste cantitati discrete din punct de vedere matematic reprezinta "cuantizarea" acelei proprietati.

De exemplu, sa presupunem ca exista o forta F care se propaga prin intermediul unor bosoni (particule purtatoare a acelei forte). Ce valori pot lua acesti bosoni? Sunt parte a unui continuu si pot lua orice valoare, gen 1,1; 1,2; 1,3; 1,4... etc sau ei pot lua doar anumite valori discrete?

Daca ar fi sa descoperim ca aceasta forta ipotetica pe care tocmai am invetat-o, "F", este cuantizata, am descoperi ca bosonii respectivi au doar anumite valori energetice - ei nu sunt parte a unui continuum cu zecimale infinite, ci iau valori concrete, discrete, clare.

In acest caz, am putea descoperi ca in loc sa poata lua valorile 1,1; 1,2; 1,3; 1,4 etc, ei pot lua doar valorile 1; 2; 3; 4 etc. Numere intregi. Nu pot lua valori intermediare, au ori valoarea 1, ori valoarea 2, dar nu au 1,1 sau 1,2 sau 1,3.

Acest lucru inseamna cuantizarea acestei forte "F" pe care tocmai am inventat-o - descoperirea faptului ca modul prin care aceasta forta se exprima prin intermediul unei particule se face prin niste cantitati discrete, si nu printr-un continuum de valori.

Nota: Pana si veziculele de neurotransmitatori din sinapsele neurale sunt cuantizate - sunt niste cantitati discrete. Deci si comunicarea neurala este cuantizata.

Revenind la Max Planck, acesta a descoperit in anul 1900 constanta ce ii va purta numele - constanta lui Planck, constanta ce va fi, apoi, pilonul principal al mecanicii cuantice. Constanta lui Planck era raportul dintre energia si frecventa unei unde electromagnetice (nu am sa intru in detalii).

Nota: Nu v-ati intrebat niciodata de ce, daca relatia dintre masa si energie este data de formula E=mc², poate avea fotonul energie? Sa nu uitam, fotonul are masa inertiala 0. Folosind formula E=mc², si inlocuind termenul pentru masa cu valoarea sa, 0, vom avea ca energia fotonului este 0. Ceea ce, evident, este incorect. Asta pentru ca energia in cazul fotonului este data de formula "E=hf", unde "h" este constanta lui Planck iar "f" este frecventa. De aici rezulta ca energia unui foton este direct proportionala cu frecventa sa.

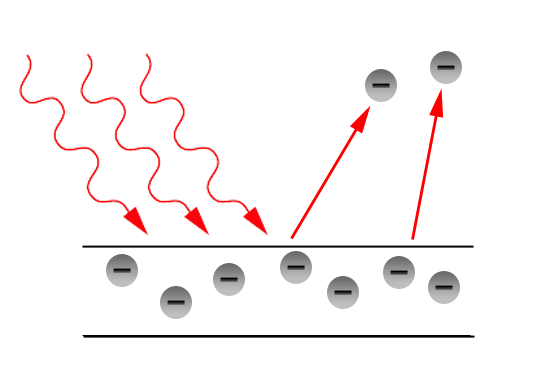
Albert Einstein s-a folosit, 5 ani mai tarziu, de acest lucru publicand o lucrare despre experimentul care va avea sa-i aduca Premiul Nobel, si anume "Efectul Fotoelectric".

Einstein a experimentat ce comportament are lumina asupra electronilor dintr-un metal atunci cand este orientata catre acesta. A descoperit ca lumina de o anumita "culoare" (frecventa) putea desprinde electroni din metal, independent de intensitatea luminii. Poti folosi lumina de o anumita frecventa, foarte putin intensa, si aceasta va reusi sa desprinda electroni din metal. In acelasi timp, poti folosi o lumina de o frecventa mai joasa, dar foarte foarte intensa, si nu vei reusi sa desprinzi niciun electron din atomii metalului. Cum putea fi acest lucru posibil?! Cum era posibil ca doar frecventa luminii sa dicteze caracterul sau ionizant, si nu intensitatea acesteia?!

Einstein a dedus din acest experiment ca lumina are un caracter de particula, iar cuantizarea undei electromagnetice se face prin intermediul fotonului. Fotonul, era, deci, particula "purtatoare" a fortei electromagnetice, fiind, de fapt, o excitatie a campului cuantic electromagnetic. Fiind un purtator de forta, fotonul este un boson (am discutat despre ce este un boson in postul meu anterior referitor la modelul standard al particulelor).

Asadar, forta electromagnetica a fost cuantizata de experimentul lui Albert Einstein, motiv pentru care a si primit Premiul Nobel.

Nota: Max Tegmark scrie, in cartea sa, "Universul nostru matematic", despre felul in care era vazuta Teoria Relativitatii la momentul in care Albert Einstein a primit Premiul Nobel:

"Pe pagina de internet nobelprize.org se poate citi ca Premiul Nobel pentru Fizica i-a fost acordat lui Albert Einstein in 1921 "pentru serviciile aduse Fizicii Teoretice si indeosebi pentru descoperirea legii efectului fotoelectric". Totusi, un coleg de-al meu suedez din Comitetul Nobel mi-a aratat odata o versiune intreaga mai putin publicata a textului de acordare a premiului. In traducerea mea de mai jos, am scris cu litere aldine hilara precautie pe care unii mocofani au introdus-o pentru a reflecta indoielile lor cu privire la teoria relativitatii, astazi unanim considerata ca una dintre cele mai mari triumfuri ale mintii omenesti:

ACADEMIA REGALA DE STIINTA DIN SUEDIA, in cadrul intalnirii sale din 9 noiembrie 1922, in conformitate cu regulamentul din 27 noiembrie 1895, dupa dorinta lui ALFRED NOBEL, a hotarat sa acorde premiul pe 1921 persoanei care a facut cea mai importanta descoperire sau inventie in domeniul fizicii, ALBERT EINSTEIN, pentru contributiile aduse Fizicii Teoretice, indeosebi descoperirea efectului fotoelectric, independent de aprecierea ca, dupa o posibila confirmare, premiul ar putea fi atribuit pentru teoria relativitatii si gravitatiei.

Asadar, descoperirile lui Max Planck si, mai apoi, Albert Einstein au pus fundatiile fizicii cuantice. Astfel, concluzia era ca natura nu era un continuum, ci mai degraba era exprimata prin niste cantitati discrete, descrise de ecuatii matematice.

Niels Bohr s-a folosit de aceste idei pentru a introduce propriul sau model atomic. El a venit cu ideea, in 1913, conform careia nu doar materia si lumina erau cuantizate, ci si anumite aspecte ale miscarii. Astfel, pentru modelul sau atomic, electronii nu puteau fi "pe orice fel de orbita", ci numai pe orbite discrete, specifice unor anumite nivele absolute de energie:

Cea mai mica orbita permisa este descrisa mai sus ca fiind n=1, iar celelalte orbite superioare ca energie sunt denumite n=2, n=3 si asa mai departe, ale caror raze sunt de n² ori mai mari decat cea mai mica.

Nota: Niels Bohr a presupus ca momentul cinetic al orbitei electronului era cuantizat, si ca acesta putea sa fie egal doar cu multipli "n" a ceea ce se cheama constanta lui Planck h redusa, definita ca h/2PI. Momentul cinetic al unui obiect ce se roteste este o masura a timpului de care este nevoie pentru a-l opri din rotit, ce indica momentul fortei mediu care trebuie folosit. Ceva ce orbiteaza intr-un cerc de raza r cu un impuls p are un moment cinetic rp.

Astfel, modelul atomic al lui Bohr nu poate colapsa deoarece cand electronul este pe orbita n=1 el nu poate cobori pe o orbita mai joasa - este cea mai joasa orbita pe care se poate afla (este orbita in care electronul are cea mai putina energie).

Electronul poate "sari" pe orbita n=2 daca absoarbe un foton cu exact acea cantitate de energie care sa fie necesara pentru un astfel de salt de pe stratul 1 de energie pe stratul 2 de energie. Dupa ce acesta petrece ceva vreme pe stratul 2 de energie, electronul vrea sa fie pe orbita cu cel mai mic nivel de energie, adica pe orbita n=1, si va sari pe aceasta orbita, eliberand un foton cu exact aceeasi frecventa ca cel pe care l-a absorbit. Astfel, energia este conservata, fotonul este eliberat iar electronul coboara inapoi pe primul strat de energie, pe care se afla inainte de absorbtia fotonului (vedem in ilustratie emisia fotonului de culoare rosie si saltul electronului de pe stratul 3 pe stratul 2).

Modelul atomic al lui Bohr explica, astfel si de ce curcubeul are "culori lipsa" in spectrul sau. Explicatia este ca gazele din atmosfera terestra absorb anumiti fotoni, cu o anumita lungime de unda, iar compozitia atmosferei dicteaza ce culori sunt absorbite de catre electronii atomilor gazelor din atmosfera si deci ce culori lipsesc din spectrul curcubeului:

Niels Bohr a primit Premiul Nobel pentru acest model al atomului in care orbitele electronilor erau cuantizate, interactionau cu fotoni de anumite energii (frecvente) pentru a face salturi intre orbite si eliberau, la randul lor, fotoni de exact aceleasi frecvente ca cei absorbiti pentru a face inapoi saltul pe stratul inferior de energie.

Problema era insa ca modelul lui Niels Bohr nu functiona decat pentru atomul de hidrogen. Pentru a-l face sa functioneze pentru celelalte tipuri de atomi, toti electronii in afara de unul trebuiau eliminati.

Asadar, ceva si mai ciudat se petrecea in povestea atomica, iar acel "ceva si mai ciudat" se va dovedi ca fiind esenta mecanicii cuantice, despre care vom vorbi in urmatorul post. Va trebui, mai intai, sa intelegem natura mecanicii cuantice, dupa care sa vedem ce fel de implicatii are aceasta natura asupra realitatii.